https://codeforces.com/contest/1189
Dashboard - Codeforces Round #572 (Div. 2) - Codeforces
codeforces.com

ㅎㅎ
학코금버
(학회 코포스터디 금요일 버추얼)
A.
0과 1의 개수가 다르면 그대로 출력해주면 되고, 같으면 맨 앞 하나를 자른 문자열을 출력하면 된다.
맨 앞 한 글자와 나머지로 string을 분리하면 각각에서의 0과 1의 개수가 다를테니까!
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n; cin >> n;
string s; cin >> s;
vector<int> count(2);
for (int i = 0; i < s.length(); i++) {
count[s[i] - '0']++;
}
if (count[0] != count[1]) {
cout << 1 << kEndl;
cout << s << kEndl;
}
else {
cout << 2 << kEndl;
cout << s[0] << ' ';
for (int i = 1; i < s.length(); i++) {
cout << s[i];
}
cout << kEndl;
}
}
B.
쓸 데 없이 두 번이나 틀렸다..
풀이를 빨리 생각해낸 게 너무 신난 바람에 별로 확인 안 해보고 제출했다..
앞으로 이러지 말아야지.
일단 수들을 정렬해놓고, 가장 큰 수가 두 번째로 큰 수와 세 번째로 큰 수의 합보다 작은지 확인한다.
만약 그렇지 않다면 문제에서 요구하는 정렬을 만들 수 없다.
만약 이를 만족하면 다른 수에 대해서는 신경 쓸 필요가 없다.
모든 수에 대해 옆에 자신보다 크거나 같은 수와, 자신보다 작거나 같지만 무조건 1 이상인 수가 있기 때문에 양 옆 값의 합이 무조건 자신보다 크다.
그래서 두 번째로 큰 수 -> 가장 큰 수 -> 세 번째로 큰 수를 출력하고, 이미 정렬된 나머지 수들을 출력하면 답이다.
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n; cin >> n;
vector<int> arr(n);
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
sort(arr.begin(), arr.end(), greater<>());
if (!(arr[0] < arr[1] + arr[2])) {
cout << "NO" << kEndl;
}
else {
cout << "YES" << kEndl;
cout << arr[1] << ' ' << arr[0] << ' ' << arr[2] << ' ';
for (int i = 3; i < n; i++) {
cout << arr[i] << ' ';
}
cout << kEndl;
}
}
C.
문제를 어렵게 생각했는데 전혀 어려운 문제가 아니다.
문제에서 특정 구간의 수들을 둘씩 짝지어서 더해나가는 걸 특별한 것 마냥 얘기했지만
그냥 결국 구간 내 수들을 모두 더한다는 의미이다.
그리고 합이 10을 넘을 때 candy가 하나씩 추가되는데
이것 또한 다 더한 후에 확인해도 전혀 문제되지 않는다.
그래서 prefix sum을 이용해서 구간에서의 합을 구하고 10으로 나누는 게 답이다.
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n; cin >> n;
vector<int> arr(n + 1);
for (int i = 1; i <= n; i++) {
cin >> arr[i];
arr[i] += arr[i - 1];
}
int q; cin >> q;
while (q--) {
int left, right; cin >> left >> right;
cout << (arr[right] - arr[left - 1]) / 10 << kEndl;
}
}
D1.
결국 못 풀었다
엄청 어려운 문제인 줄 알았는데
사실 효규가 빨리 풀어서 구현이 복잡하거나 어려운 문제가 아닐 것 같긴 했지만
이렇게 간단할 줄은 몰랐다
degree가 2인 노드가 존재하면 NO인 것이다...
degree가 1인 노드는 leaf node라는 뜻이니까 문제될 게 없고
degree가 3 이상이면 항상 모든 경우가 가능하다.
학회 스터디에서 끝나고 풀이 얘기할 때 이를 증명했는데
간선이 세 개라고 가정하고, 각각은 리프 노드와 연결되어 있으며, 각각의 가중치가 x, y, z라고 할 때
두 간선을 골라서 값을 더하는 과정을 세 쌍에 대해 시행할 수 있다.
이때 더하는 값을 각각 a, b, c라고 하면
a + b = x
b + c = y
c + a = z를 만드는 a, b, c는 항상 존재한다.

(기분 좋아서 그려봤다)
이와 다르게 degree가 2인 노드는 a = x, a = y인 a가 항상 존재하는 건 아니므로 불가능하다.
그리고 degree가 3보다 큰 노드에 대해서는 그 노드에 연결된 간선들 중 3개를 골라서 해당 작업을 한다고 생각하면 되므로 모두 가능하다.
진짜...신기했다
효규야 수학과 가라
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n; cin >> n;
vector<int> degree(n + 1);
for (int i = 0; i < n - 1; i++) {
int u, v; cin >> u >> v;
degree[u]++;
degree[v]++;
}
bool ans = true;
for (int i = 1; i <= n; i++) {
if (degree[i] == 2) {
ans = false;
break;
}
}
cout << (ans ? "YES" : "NO") << kEndl;
}D2는 '간선에 더하는 값이 오직 정수일때 가능한가?'가 문제인데
위에서 말한 것처럼 degree가 3인 노드에 대해서 a, b, c를 구할 때부터 정수가 아닐 수 있고
degree가 3보다 큰 경우는 그 중 세 개의 간선을 골라서 위 작업을 한다고 생각해본다면
매우매우 복잡한 문제가 된다.
E.
끝나고 풀이 공유할 때 gumgood님께서 풀이해주셨다

이를 만족하는 쌍의 개수를 구하는 문제인데

이렇게 양 변에 두 값의 차를 곱하고 정리하면
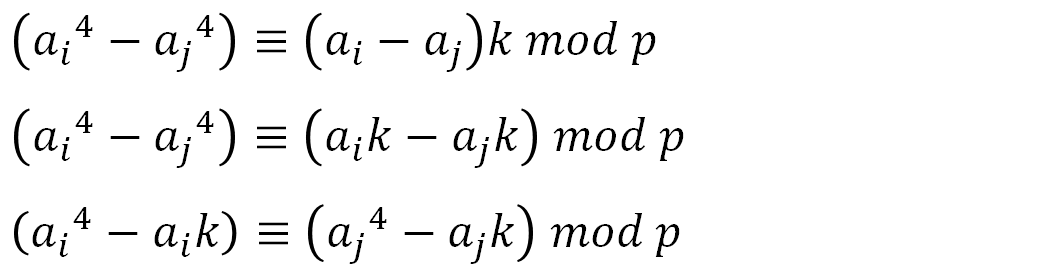
결국

의 값이 같은 쌍의 개수를 구하는 문제가 된다..
엄청나다....!!!
ll nC2(int n) {
return n * (n - 1) / 2;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int n, p, k; cin >> n >> p >> k;
vector<ll> arr(n);
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
map<ll, int> cnt;
for (int i = 0; i < n; i++) {
ll result = 1;
for (int j = 0; j < 4; j++) {
result *= arr[i];
result %= p;
}
result = (result - (arr[i] * k) % p + p) % p;
cnt[result]++;
}
ll answer = 0;
for (auto iter = cnt.begin(); iter != cnt.end(); iter++) {
answer += nC2(iter->second);
}
cout << answer << kEndl;
}